Integer 3 and Beyond
- Ake "Dojomaster" Takahashi
- Apr 1, 2019
- 5 min read
Why 3?
According to the Pythagoreans, 3 was the noblest of all digits.
1. The first odd prime number
2. first Fermat prime F{n} = 2^{2^{n})+1 3, 5, 257, …
3. first Mersenne prime Mn = 2^n − 1 3, 7, 31, 127, ...
4. first lucky prime a natural number in a set which is generated by a certain “sieve”, defining sieve is called "the sieve of Josephus Flavius” 1, 3, 7, 9, 13, 15, 19... on the third pass
5. genetic information is encoded in a triplet codon system
6. white light is composed of the mixture of the three additive primary hues: red, yellow, and blue
7. Plato’s Tripartite soul: Rational, Libidinous, Spirited
8. Francis Galton’s 3 genius traits: Intellect, Zeal, Power of Working
9. William Herbert Sheldon’s body types: Endomorph, Mesomorph, Ectomorph,
10. Mark Twain's 3 lies: Lies, Damned Lies, and Statistics,
11. Witness Stand truths: The Truth, The Whole Truth, Nothing but the Truth
12. A Triangle has 3 angles, 3 vertices, and 3 edges
13. Gauss proved that every integer is the sum of at most 3 triangular numbers.
14. A circle can be drawn through any 3 points not on a straight line.
15. A number is divisible by 3 if and only if the sum of its digits is divisible by 3.
16. Vinogradov theorem states all sufficiently large odd numbers are the sum of at most three primes.
17. The smallest magic square is of order 3.
18. It is the first member of an arithmetical progression of 3 primes 3 - 5 - 7
19. In English the sequence once-twice-thrice goes no further.
20. In Greek mythology there were 3 Fates, 3 Furies, 3 Graces, 3 x 3 Muses, and Paris had to choose between 3 goddess.
21. The first case of Fermat’s Last Theorem x^3 + y^3 = z^3
22. Johnson’s Theorem: if three congruent circles intersect in a single point, the other three pints of intersection must lie on a circle congruent to the first three.
23. Napoleon Theorem deals with the centers of 3 different triangles.
24. The magical point in the interior of the triangle is known as the “Fermat point” signifying the sum of three distances is minimum.
25. n is called the super-3 number when 3n^3 contains 3 consecutive three 3s
"What I tell you three times is true." - Lewis Carroll, The Hunting of the Snark, 1876 (Charles Dodgson)
Let’s start this section with a super-3 number which is an integer n such that 3n^3 contains 3 consecutive 3s in its decimal representation. The first of its kind is n = 261.
3(261)^3 = 3 (261)(261)(261) = 53338743
Some of the Super-3 numbers are: 462, 471, 481, 558, 763,… According to Pickover, 471, 4710, 47100 are all super-3 numbers. We do not know the practical application for the Super-3 numbers yet, but this topic is presented because of the following mind bender problems the MathDojo came up to challenge your creative thinking.
Let’s test your mettle. Using three 3s and mathematical operations, find the expressions equal to 20. Here are some solutions.

Another 3 topics we like to discuss are usually not covered in regular math classes. They are 1) Isoperimetric inequality, 2) Viviani Theorem and Barycentric coordinates 3) Reuleaux triangle.
From time immemorial we were interested in 3 main geometric figures: circles, squares, and triangles. The following famous calligraphic drawing was done by Sengai (1750-1838) with each form touching and showing some dynamic connection.

Today we have a puzzle and a USB connection diagram.
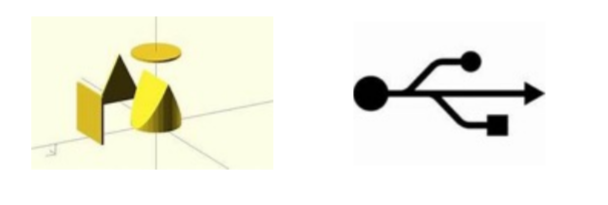
Yet we do not have a single word to describe the solid figure that can go through a triangle hole, a square hole and a circular hole. So we at MathDojo want to call it a tri-squircle.
Given three figures a circle, a square,and a triangle with all of them with the same perimeter, which figure will contain the largest area? This is an isoperimetric inequality problem. We can use a planimeter to determine the perimeter of each figure so that they are approximate equal. Here is the inequality formula. The formula is equal only for the circle.
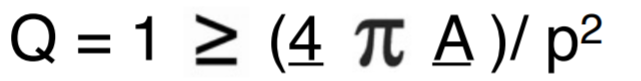
The letter Q is used in honor of Queen Dido who started the isoperimetric idea. According to a legend about the foundation of Carthage (around 850 B.C.), Dido purchased from a local king the land along the North African coastline that could be enclosed by the hide of an ox. She sliced the hide into very thin strips, tied them together, and was able to enclose a sizable area which became the city of Carthage. Dido's story has been told throughout history. It is a very engaging and intriguing one and everyone is encouraged to find out the legend and legacy of Dido from its telling in Virgil’s Aeneid.
Do you know what {3}, {3,3} and {3,3,3} mean? If you say they are sets. You are close, but no cigars! The first one represents an equilateral triangle and the second one is the regular tetrahedron (one of the Platonic solids), third one is pentatope which is the four-dimensional tetrahedron. In geometry, the Schläfli symbol is a notation of the form {p,q,r,...} that defines regular polytopes and tessellations.The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli who generalized Euclidean geometry to more than three dimensions and discovered all their convex regular polytopes.
The Schläfli symbol is a recursive description starting with {p} for a p-sided regular polygon that is convex. For example, {3} is an equilateral triangle, {4} is a square, {5} a convex regular pentagon and so on. A regular polyhedron that has q regular p-sided polygon faces around each vertex is represented by {p,q}. For example, the cube has 3 squares around each vertex and is represented by {4,3}. A regular tetrahedron is {3,3}. The pentagram is represented by {5/2}.
One of the important theorems related to an equilateral triangle is Viviani Theorem. It states that the sum of the distances from any interior point to the sides of an equilateral triangle equals the length of the triangle's altitude.
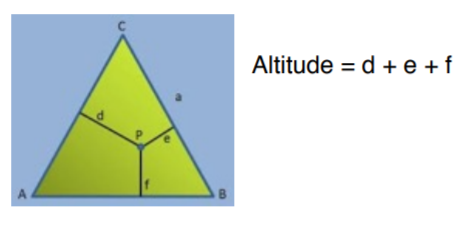

Viviani's theorem means that three sides of an equilateral triangle give coordinates for making ternary plots with Barycentric coordinates, such as flammability diagrams. A ternary plot, (ternary graph, triangle plot, simplex plot, Gibbs triangle or de Finetti diagram) is a Barycentric plot on three variables which sum to a constant. It graphically depicts the ratios of the three variables as positions in an equilateral triangle. Ternary plots are a way of displaying the distribution and variability of three-part compositional data. (For example, the proportion of sand, silt, and clay in soil or the proportion of three chemical agents in a trial drug.) It is used in physical chemistry, petrology, mineralogy, metallurgy, and other physical sciences to show the compositions of systems composed of three species. In population genetics, it is often called a de Finetti diagram. In game theory, it is often called a simplex plot. Three Component Mixtures in Pharmaceuticals and its Applications use Ternary plots that are useful tools for analyzing compositional data for 3 materials.

The last of the three topics we want to discuss is Reuleaux Triangles. A curve of constant width constructed by drawing arcs from each polygon vertex of an equilateral triangle between the other two vertices. It is important that you do not get confused with a spherical triangle which is drawn on the surface of a sphere. Click on the center to see the rotation.
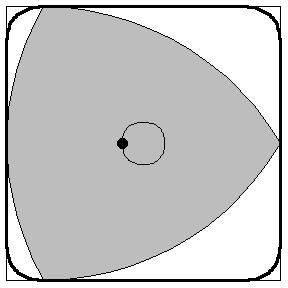
Because it can be rotated inside a square, as illustrated on above, it is the basis for the Harry Watt square drill bit.

References:
Geometry Junkyard
Eric Weisstein CRC Concise Encyclopedia of Mathematics
Wikipedia
William Hartston The Book of Numbers
David Wells The Penguin Dictionary of Curious & Interesting Numbers
Clifford Pickover Mazes for the Mind: Computers and the Unexpected
Clifford Pickover Passion for Mathematics
Emmanuel Tsukerman Isoperimetric Inequalities and the Alexandrov Theorem






Comments