Magic Squares and Beyond
- Ake " Dojomaster" Takahashi
- Mar 25, 2019
- 6 min read
Unlike the Punnet Square which is a square diagram that is used to predict the genotypes of a particular cross or breeding experiment limited to 2 x 2 or 4 x 4, the Magic Square is a square that is divided into cells, filled with numbers in particular arrangements that were once thought to have special, magical properties. Originally used as religious symbols, they later became protective charms; and finally, when the original meanings were lost, people considered them mere curiosities or puzzles—except for some Western mathematicians who continue to study them as problems in number theory. The most famous one is a 3 x 3 magic square (order 3) containing numbers 1 - 9 with a constant sum of 15. 15 = (1+2+3+4+5+6+7+8+9)/3 or 1/2(n)(n^2 +1). n = order # . The magic sum simply means every row, column, and diagonal add up to the same number. So can you fill the blanks?
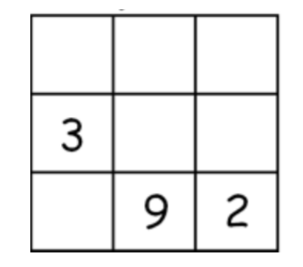
There is only one 3 x 3 magic square. However, there are 880 magic squares for order 4. ( 4 x 4 ) Can a 3 x 3 magic square be constructed with nine distinct square numbers? In 1996 this question became famous when Martin Gardner, renowned recreational mathematician, offered $100 to the first person to construct such a square. Today, this problem is not yet solved.

Probably the most famous magic square is the one that appears in the fantastic engraving of Melencolia (1514) by Albrecht Dürer. The number 1514 appears in the engraving. 1 and 4 on the bottom represent the alphabetical order of his initials. The magic sum is 34. There are five 2 x 2 squares with the sum of 34.

Birthday Magic Squares
Another 4 x 4 magic square is the Birthday Magic Square, created by Indian mathematician Srinivasa Ramanujan. He produced a super magic square. The top row is his birthdate (22, December, 1887). This is a super magic square because not only do the rows, columns, and diagonals add up to the same number, but the four corners, the four middle squares (17, 9, 24, 89), the first and last rows two middle numbers (12, 18, 86, 23), and the first and last columns two middle numbers (88, 10, 25,16) all add up to the sum of 139. Check out his magic square below.

The birthday magic square is a fun activity to try. First, try it on your own to see if you can create your own birthday magic square without any help. Just grab a pencil, paper, and calculator. If you are unable to create your own birthday magic square, you can follow Ramanujan’s Magic Square Generator.
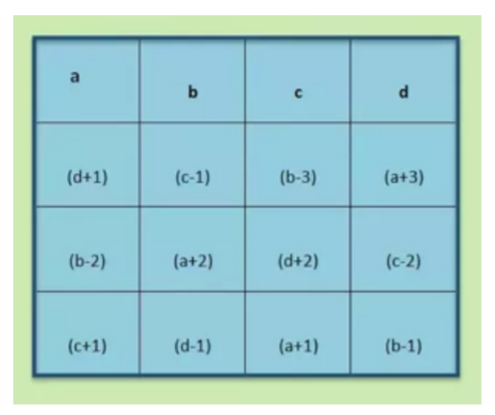
Euler Squares or Latin Squares
With the recent popularization of Sudoku, interest in related mathematical games such as magic squares and Latin squares has also been revived. Sudoku puzzles are a special case of Latin squares; in fact any solution to a Sudoku puzzle is a Latin square. A Latin square is a square grid filled with symbols in such a way that each symbol occurs once and only once in each row or column. Here is an example of an Euler Square.

Latin squares are used in the design of experiments, tournament scheduling, and constructing magic squares.
Benjamin Franklin’s Magic Squares
Ben Franklin worked on magic squares because he was so bored with meetings. His 8 x 8 magic square is well known, but his 16 x 16 magic square is truly fantastic. Although the diagonals of his square do not sum to 2056, there are many other magical properties. It has been noted Franklin as having said, "it is the most magically magical of any magic square ever made by any magician.” All the rows and columns sum to the number 2056, but that is not all. The sixteen entries in every 4x4 square sum to 2056. Even bent diagonals sum to 2056.
Geomagic Squares
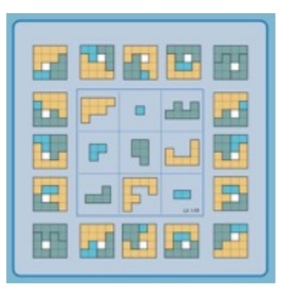
Lee Sallows is an expert on the theory of magic squares. He also invented a golygon which is any polygon with all right angles (a rectilinear polygon) whose sides are consecutive integer lengths.

Sallows invented geomagic squares. Here is a 3 × 3 geomagic square. The 3 pieces occupying each row, column and diagonal pave a rectangular target, as seen at left and right, and above and below. The 9 pieces are called decominoes.
Magic Hexagons
The magic squares can jump to different kinds of number mazes such as a Magic Hexagon. It is interesting to note that the number in the center is 5 just like the 3 x 3 magic square. The Magic Sum in this case is 38. This is still order 3.

Can you fill the blanks without looking at the one on the left?
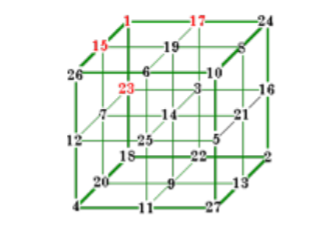
The Perfect magic cube is a cube in which not only the columns, rows, pillars, and main space diagonals, but also the cross section diagonals sum up to the cube's magic constant. Cubes of orders two to four can be proven not to exist. The magic cubes of order 5, 6, 7, 8 ,9, 10, and 11 were discovered. The Rubik’s Cube was originally called the Magic Cube. The goal is to get each side the same color. What happens if each side of the cube is labeled 1-9 on white color to get 3 x 3 magic square on all 6 sides? You are not concerned with space diagonals in this case. Interesting?
Area Magic Squares
Instead of filling magic squares with numbers, William Walkington started an interesting discussion as to how to create magic squares with cells that had the same areas as their numbers. One of them is a graphic design for a 2017 seasonal greetings card, showing a magic square with approximate areas that was constructed by William Walkington (2016).
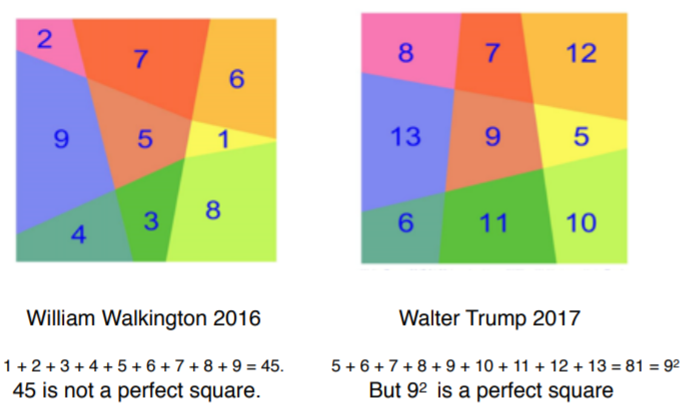
Using the number sequence with the sum = 9^2, Walter Trump (2017) was able to construct the area magic square on the right. Some experts were able to establish some formulas, so that sum of the numbers in magic squares always becomes a perfect square.
Variations:
Let’s look at the 4 x 4 squares with numbers 1- 16.
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
Pick any number from the square and then circle it. Cross out the numbers vertically and horizontally that belong to the circled number. Next you can pick any number from uncrossed numbers. Repeat the same rule. Circle the number and cross out the vertical and horizontal numbers associated with the second circled number. You then pick the third uncrossed number and circle it. You will find out the sum of all uncrossed numbers is 34, which is the same as the magic sum of 4 x 4 magic square.
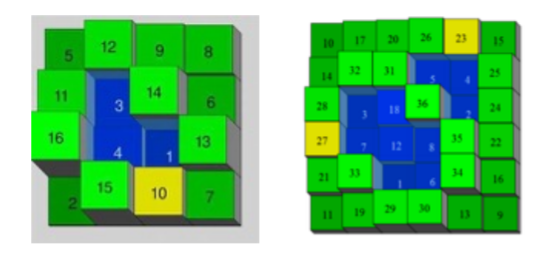
Magic Squares with Water Retention
In 2007, the idea of studying the water retention on a magic square was proposed.This is a 3D magic square with the number indicating the height. In 2010, a competition at Al Zimmermann's Programing Contests produced the presently known maximum retention values for magic squares order 4 to 28. This is a very difficult combinatorial optimization problem.
15 puzzles
These are sliding puzzles that consist of numbers 1 to 15.

To solve the puzzle, the numbers must be rearranged into order. The puzzle was "invented" by Noyes Palmer Chapman, a postmaster in Canastota, New York. Chapman had applied for a patent on February 21, 1880. However, that patent was rejected. Sam Loyd, recreational mathematician, claimed from 1891 until his death in 1911 that he invented the puzzle. He did not. However, he was the one who fueled the interest in the game by offering $1000 prize for anyone who could provide a solution for achieving a particular combination specified by Loyd, namely after reversing the 14 and 15 on the figure on the right.
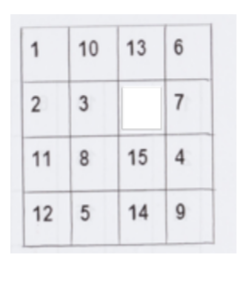
The very useful application of the sliding game is to move pieces to this pattern on the right. Consider the empty space to be 16. Now you have all the solutions to the Prime Neighbors Sequence. You may start with any number, add a neighbor number to create a prime number. For example: 1, 10, 13, 6, 7, 16, 3, 2, 11, 8, 15, 4, 9, 14, 5, 12 .or you can start with 16. 16, 15, 14, 9, 4, 7, 6, 13,10, 3, 8, 5, 12, 11, 2, 1.
A Base 2 Game
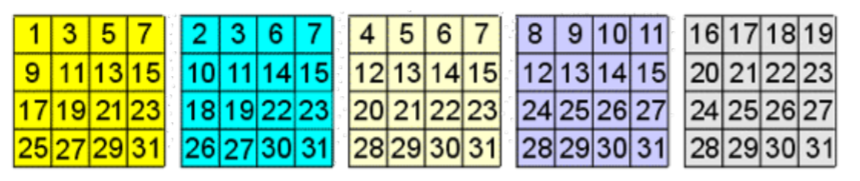
To play this game you have five sheets of paper, each of a different color. Each sheet contains numbers between 1 and 31. Ask someone to think of a number between 1 and 31, inclusive, but not to tell you what the number is. Ask them to tell you on which sheets does their number appear. You can then tell them what their number is. How do we do this? Can you figure it out? Hint: use the numbers on the upper lefthand corner.
Another game you may want to play is called the BinaryPuzzle. You use only 0 and 1 to fill the squares. You can go to binarypuzzle.com to play the game online.

From Conjecture to Theorem In 1844 the mathematician Eugène Charles Catalan conjectured:
x^a - y^b = 1 for a, b > 1, x, y > 0 is x = 3, a = 2, y = 2, b = 3
Preda Mihăilescu proved in 2002 that this is the only case of two consecutive powers. That is to say, that the only solution in the natural numbers of 3^2 - 2^3 = 1 So the conjecture became the theorem.


References:
Clifford Pickover The Zen of Magic Squares, Circles, and Stars 2002
Arthur Benjamin and Ethan Brown “Challenging Magic Squares for Magicians” (The College Mathematics Journal, March 2014, pp. 92– 100).
:K.Thirumurugan, Birthday Magic Square MathsTimes.com
Johan Ofverstedt Water Retention on Magic Squares http://urn.kb.se/ resolve?urn=urn:nbn:se:uu:diva-176018
Inder J. Taneja Perfect Square Sum Magic Squares RGMIA Research Report Collection, 20 (2017),
Echion, KvK 50713795, the Netherlands. info@binarypuzzle.com






Comments